Areal af trekant
Vi betragter en Δ ABC , der ikke nødvendigvis er retvinklet.
Vinkel C kan være spids, ret eller stump. (Spids betyder under 90° og stump betyder over 90°)
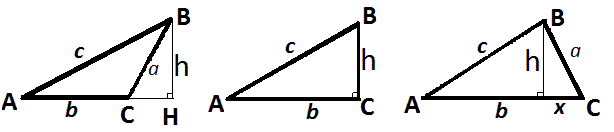
Bemærk: I figuren helt til venstre bliver vinkel BCH = 180°- vinkel C,
og derfor er Sin(vinkel BCH) = (C)
Delopgave 17
Hvad bliver arealet af Δ ABC uanset om vinkel C er stump, ret eller spids?
Svar:
T = ½ h ·
Delopgave 18
Vi vil gerne ændre formlen, så h ikke indgår.
Ved at betragte tegningen længst til højre og den lille retvinklede
trekant, der afgrænses af h, a og x, ses at h kan erstattes af a·Sin C.
Det gælder også i den midterste tegning, da C her er 90° og Sin C derfor er 1.
Ved at betragte tegningen længst til venstre og den lille retvinklede trekant, hvor
h er katete, ses at h også her kan erstattes af a·Sin C, fordi Sin(vinkel BCH) = Sin C
Udnyt dette og skriv en formel for trekantens areal, hvor h ikke indgår.
Svar:
T = ½ ab
Delopgave 19 og 20 og 21 og ...
Arealet kan således udtrykkes ved 2 sider og en vinkel i trekanten.
Da det ikke kommer an på hvilken vinkel, der indgår, kan formlen skrives
på 3 måder ved bogstavombytning. Gør det.
Svar:
T = ½ bc = ½ ac = ½ ab
Sinusrelationerne
Ovenstående ganges igennem med 2:
2T = bc = ac = ab
Delopgave 25 og 26 og 27 og ...
Divider med abc.
Svar:
Dermed er reglen bevist;
men bemærk, hvis man finder sinus til en vinkel fx ved hjælp af sinusrelationerne,
kan der være 2 muligheder for vinklen.
Delopgave 31 og 32
Hvor mange grader er vinkel v, hvis Sin(v)=0,5 og v er spids? (Helt tal)
Svar:
v = ° og hvis v er stump? (Helt tal) v = °
Cosinusrelationen (Den udvidede Pyhagoras)
Her skal vi se, hvordan man finder en side i en vilkårlig trekant ud fra de andre sider og en vinkel.
Delopgave 33 og 34 og 35 og ...
Skriv Cosinuisrealtionen.
Svar:
I enhver trekant ABC gælder: c² = a² + b² –
Bevis:
Vi betragter en vilkårlig Δ ABC
Der er 3 muligheder.
1) Vinkel C = 90°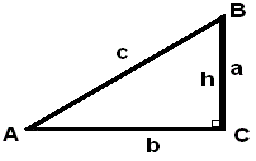
Højden fra B er sammenfaldende med siden BC.
Da vinkel C = 90°, er Cos C =
og formlens sidste led får værdien
Formlen gælder således på grund af Pythagoras sætning for retvinklede trekanter.
|
2) Vinkel C er spids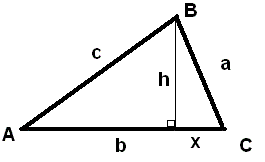
Højden fra B er inde i treklanten.
Det gælder om at finde et udtryk for c².
Siden c indgår i den retvinklede trekant, der på tegingen er til venstre for højden h.
Ved Pythagoras fås: c² = (b-x)² + ²
Men vi vil gerne udtrykke c² alene ved vinkler og sider i selve trekant ABC, så x og h skal væk. x og h indgår i den retvinklede trekant til højre for højden, så
vi kan finde x ud fra formlen: Cos C = x/a <=> x = a*, og
vi kan finde h ud fra formlen: Sin C = h/a <=> h = a* Derved får vi, c² = (b - a* )² + ( a* )² = b² + a²*Cos²C - 2* + a²*Sin²C Vi kan sætte a² uden for parentes og får c² = a²(Cos²C+Sin²C) + b² - 2* Ved anvendelse af idiotformlen fås: c² = a² + b² - , hvilket skulle vises. |
3) Vinkel C er stump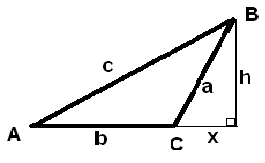
Højden fra B er uden for trekanten.
Det gælder også her om at finde et udtryk for c².
Siden c indgår i den store retvinklede trekant, der på tegingen er til venstre for højden h.
Ved Pythagoras fås: c² = (b+x)² + ²
Men vi vil også her udtrykke c² alene ved vinkler og sider i selve trekant ABC, så x og h skal væk. x og h indgår i den lille retvinklede trekant til venstre for højden, så
vi kan finde x ud fra formlen: Cos(180°- C) = x/a og
vi kan finde h ud fra formlen: Sin(180°- C) = h/a Da Cos(180°- v) = -Cos(v) fås: Cos(180°- C) = x/a <=> - Cos C = x/a <=> x = ( - a* )
Da Sin(180°- v) = sin(v) fås: Sin(180° - C) = h/a <=> Sin C = h/a <=> h = a* Derved får vi: c² = ( b + ( -a* ))² + ( a* )² = ( b - a* )² + ( a* )² = b² + a² * Cos²C - 2* + a² * Sin²C Vi kan sætte a² uden for parentes og får c² = a²(Cos²C+Sin²C) + b² - 2* Ved anvendelse af idiotformlen fås: c² = a² + b² - , hvilket skulle vises. |
Delopgave 54
Isoler Cos C i Cosinusrelatonen.
Svar: